3章 後半
3.5 並列データ管理パターン
- データへの並列アクセスを体系化するには、いくつかのパターンが使用される。
- 複数のワーカーが同じデータを変更するタイミングとその方法を把握することが重要。並列データ・アクセス・パターンのほとんどは、共有データの変更を回避するか、構造化された方法でのみ変更を許可する。
- 例外的に、スキャッター・パターン(scatter pattem)のいくつかのバリエーションは、競合状態の解決と回避に使用できる。これらのパターンの一部は、分割など、データ局所性を最適化する上でとても重要で、安全かつ並列に変更できる独立した領域を作る。
3.5.1 パック
- パックパターンはコレクション中の未使用の空間を排除することができる。falseとマークされているものを破棄し、trueとマークされた残りの要素は入力データ・コレクションと同じ順序で連続したシーケンスに配置される。
- パックは、特にマップとほかのパターンを融合して不要な出力を排除する際に役立つ。
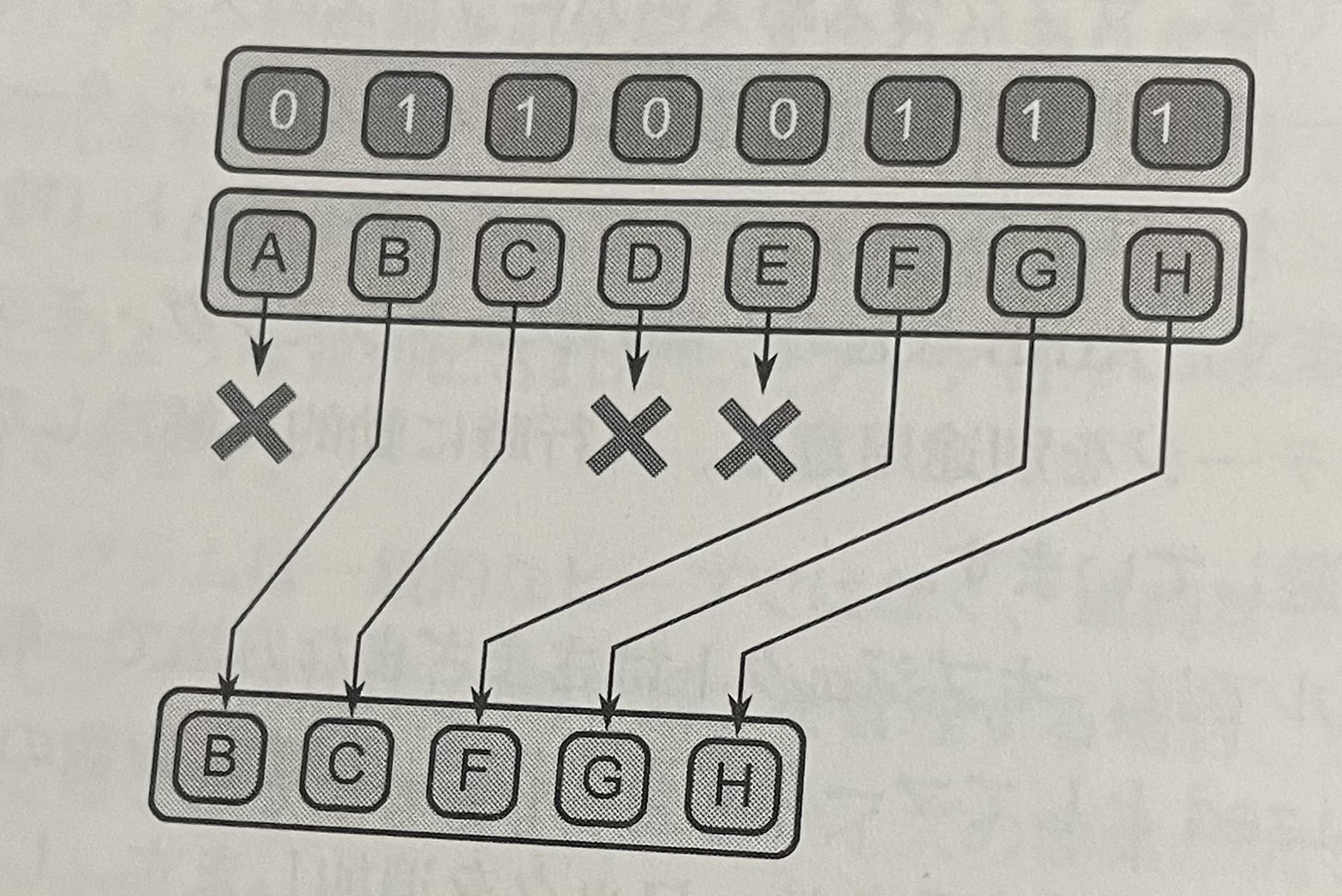

図1
- パックパターンは使用されてない要素は破棄されて連続した残りのシーケンスに要素がパックされる。
- パック操作の逆であるアンパックも便利。アンパックはパック操作によって取り出された要素をデータ・コレクションに戻す動作。
3.5.2 パイプライン
- パイプライン・バターン(pipeline patem) は、タスクを生産と消費(producer-consumer)関係に当てめる。概念的には、パイプラインのすべてのステージは一度にアクティブになり、各ステージはデータの流れに従って更新されるステートを維持。
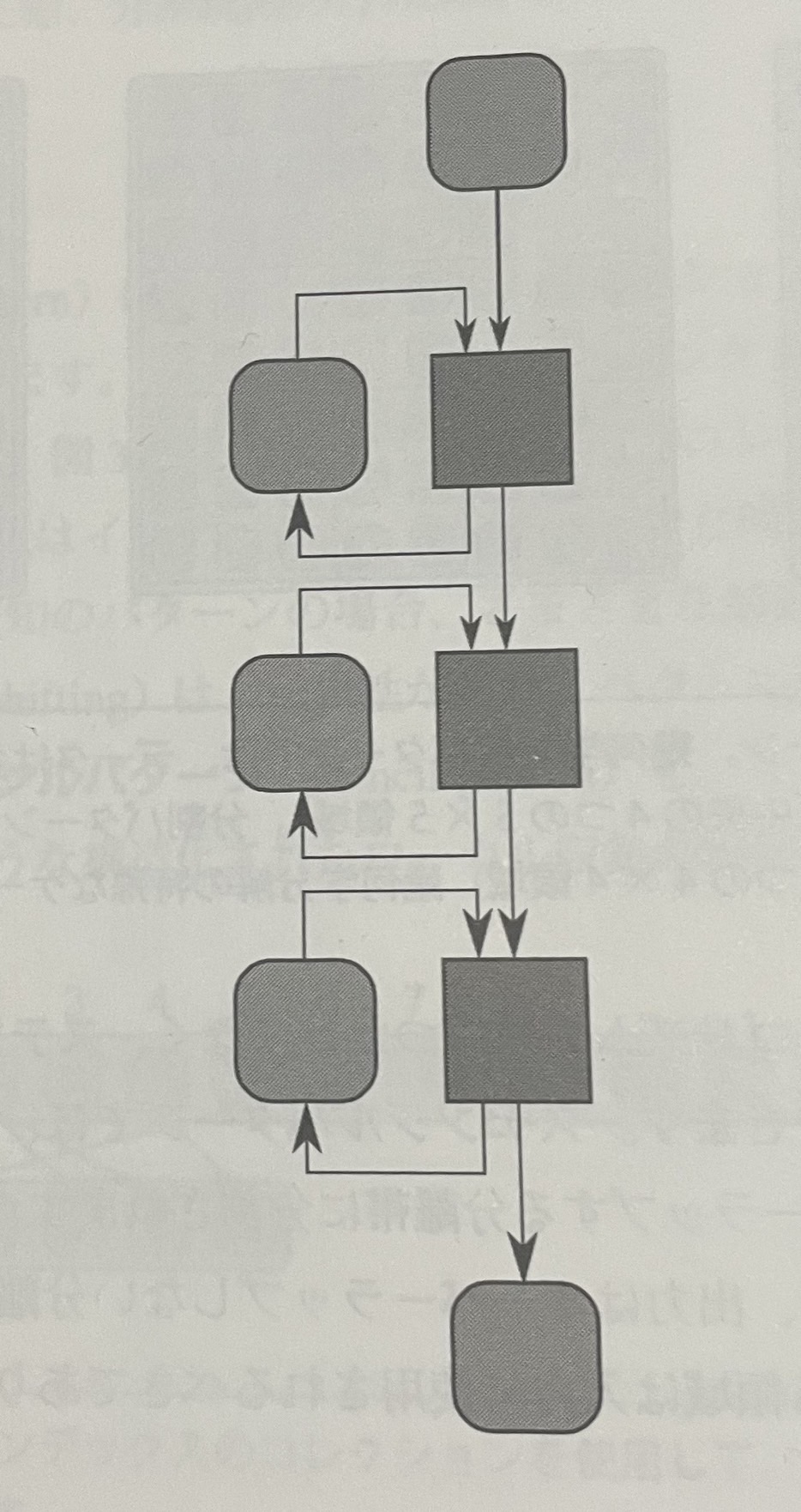
 図2
図2
- パイプライン・パターン。ステージは生産と消費関係に当てはめられ、各ステージはステートを維持できるため、後続のステージの出力が先行するステージの出力に依存することができる。
- パイプライン・パターンは、可変圧縮率のコーデック、ビデオ処理および映像合成、スパムフィルターなどで使用される。
3.5.3 幾何学分解
- 幾何学分解パターン(gcometric decomposition pattem) は、データをサブコレクションに分割する。サブコレクションとはサブコレクションとは、ソフトウェア配布の目的で他のコレクションに関連付けられたコレクション。また、特定のドキュメントに関連付けられたコレクションであることもある。
- 一般に、サブコレクションはオーバーラップすることができ、図3円央の例のように、出力がオーバーフップしない領域に分割できれば、各サブ領域は互いに十渉することなく独立して並列タスクを処理できる。
- 図3の右の例のような、オーバーラップしないサブ領域の特殊なケースを分割パターンと呼ぶ。
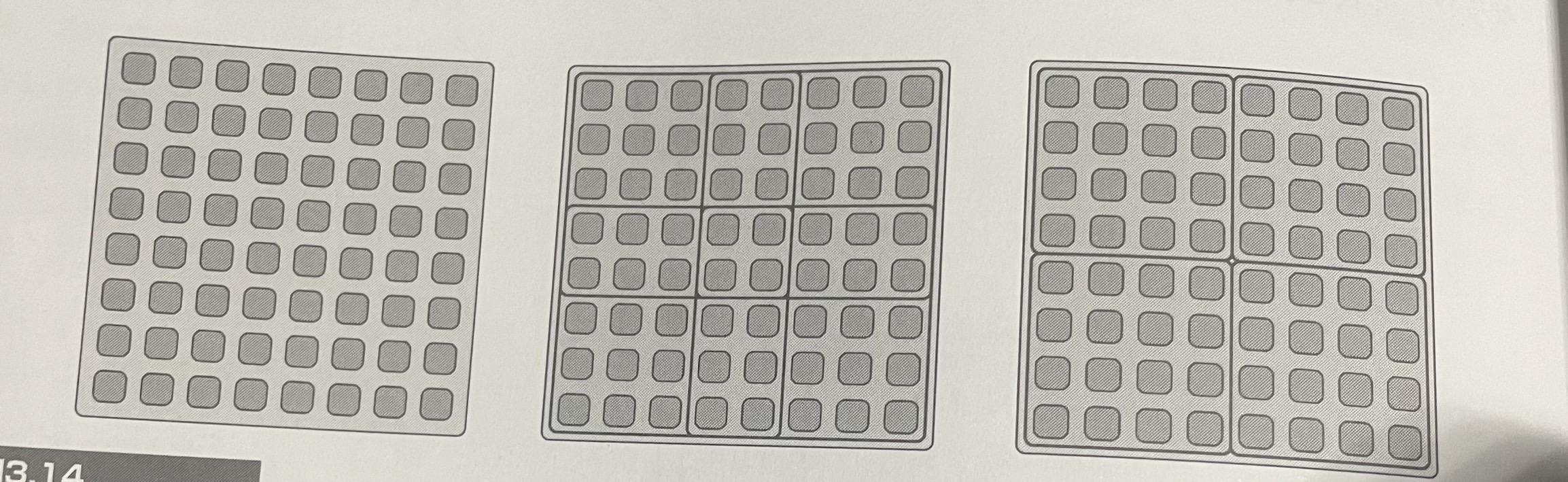
 図3
図3
- 幾何学分解と分割パターン。幾何学分解パターンでは、データはオーバーラップしている可能性がある養成に分割される(中央の4つの5X5領域)。分割パターンは、領域がオーバーラップしない領域に分割される(右の4つの4x4領域) 幾何学分解の特殊なケースである。
- 分割パターンは、分割統治アルゴリズムで役立つだけでなく、ステンシルパターン(stencil paltem)を効率良く実装するのにも使用できる。ステンシルパターンでは、一般に、隣接値がアクセスできるように、入力は部分的にオーバーラップする分離帯に分割される(一般的な幾何学分解)。ただし、独立して安全に書き込めるように、出力はオーバーラップしない分離帯に分けられます(つまり、分割)。一般に、オーバーラップする領域は入力に使用されるべきであり、出力はオーバーラップしない 領域に分割されるべきです。
- 幾何学分解は必ずしもデータを移動するわけではない。たいていは、別の「ビュー(視点)」の構成を提供するだけ。
3.5.4 ギャザー
ギャザーパターン(gather patter) は、インデックスのコレクションを使用して、別のデータ・コレクションからデータを読み込む。ギャザーは、マップとランダムなシリアル読み込み操作の組み合わせと見なすことができます。出カコレクションの要素型は入カデータ・コレクションと同じだが、形状はインデックス・コレクションと同じ。コード生成時にインデックスの配列が固定されるか、既知のパターンの場合、さまざまな最適化が可能。例えば、配列中のデータの左または右シフト(shifling)は、一買性があり、ベクトル演算を使用して高速化できるギャザーの特殊ケースである。ステンシルパターン(stencil pattern)も、マップの各要素を一貫性のある方法で収集する。そして、そのような構造化されたローカル収集の実装には固有の最適化がある。
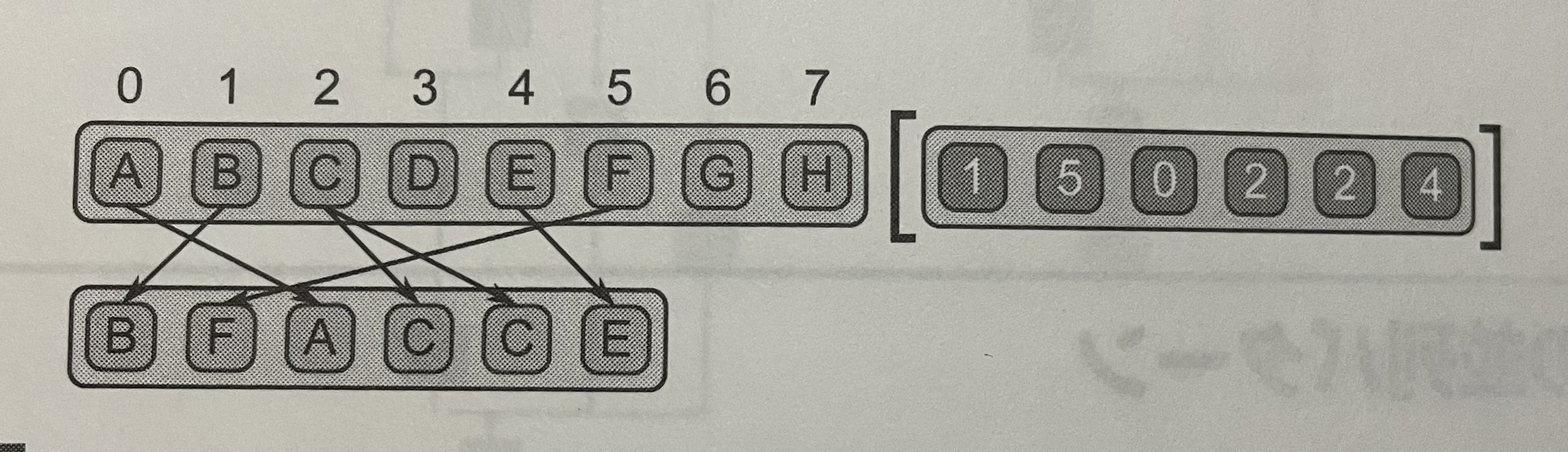

図4
3.5.5 スキャッター
- スキャッター・パターン(scatter pattern)は、ギャザーパターンの逆。一連の入力データとインデックスを使用して、入力の各要素を読み込む代わりに、指定された位置へ書きこむ。スキャッターは、マップとランダムなシリアル書き込みパターンの組み合わせと見なすことができる。
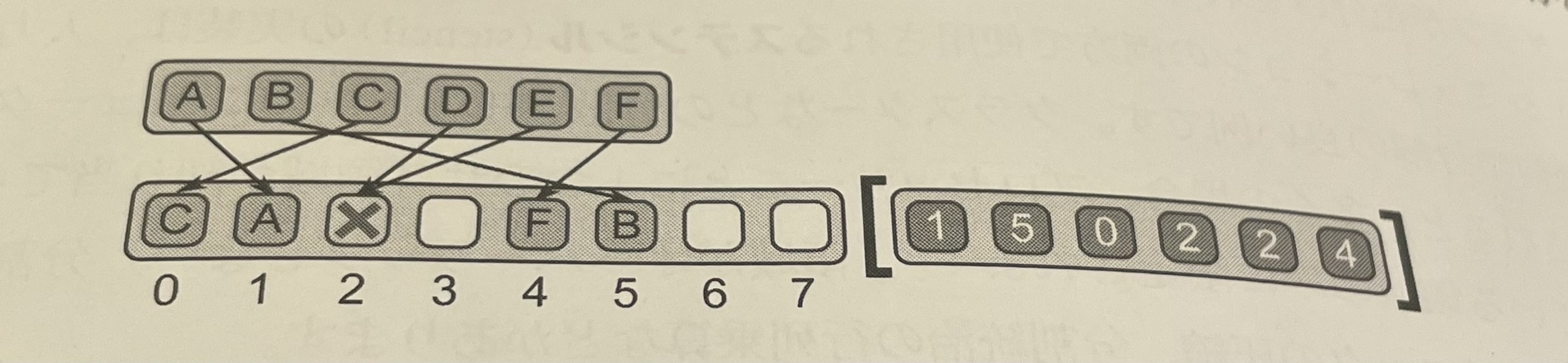
 図5
図5
- スキャッター・バターン。アドレスのコレクションで指定された位置にデータ・コレクションが書き込まれる。
- スキャッターの純粋な定義では、書き込みアドレスが重複する場合、競合状態となる可能性がある。一般的に、いずれかの値が正しく書き込まれることを仮定することすらできない。このような重複を衝突(coliston)と呼ぶ。
- スキャッターの定義を完全なものにするには、このような衝突が発生した場合の対応を定義する必要がある。
3.6 ほかの並列パターン
この節では、実際によく使用されているものの、コード例を掲載していない他のパターンを説明している。これらのパターンの一部は、すでに説明したパターンの拡張または詳細を詰めたものである。
3.6.1 スーパースカラー・シーケンス
スーパースカラー・シーケンス・パターンsuperscalar sequence pattern)では、通常のシリアルシーケンスのように、タスクのシーケンスを記述する。例として、次のコードについて考える。シーケンスパターンとは異なり、スーパースカラー・シーケンスでは、データ依存にのみ基づいてタスクを順守付ける必要があり[ERB+10、TBRG10、KLDB10]副作用がなければ、システムはタスクを別に実行したり、ソースコードと違う順序で実行できる。
1 2 3 4 5 6 7 8 | |
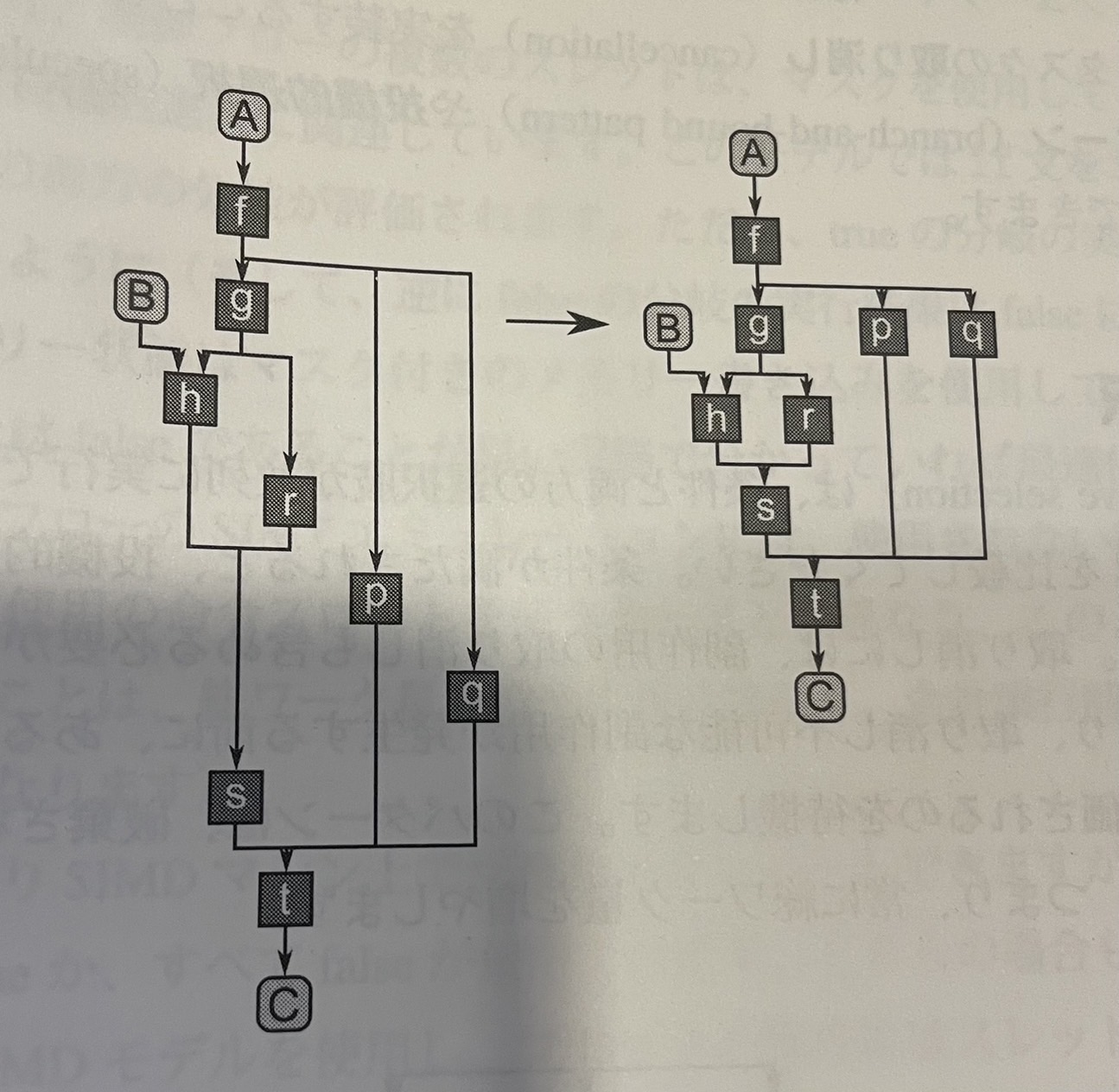
 図6
図6
スーパースカラー・シーケンスは、データ依存にのみ基づいて処理の順序を決定する。左は、シーケンスパターンを使用して、コードのシリアル実装のタイミングを示したもの。これをスーパースカラー・シーケンスのグラフとして解釈した場合、右のようにタスクを同時に実行できる可能性がある。 ここで問題となるのは、「データ依存が満たされる限り」という部分である。つまり、このパターンを使用するには、タスク・スケジューラーがすべての依存を把握していなければいけない。
3.6.2 フューチャー
- フューチャー(future)パターンはフォーク・ジョインと同じ階層パターンを実装できるが、より一般的で複雑なタスクグラフの実装にも使用される。
- フォークジョインの詳しい説明は後の方に書いてある。
- 概念的には、フォーク・ジョインはタスクのスタックベースの割り当てのようなもので、フューチャーはタスクのヒープ割り当てのようなものである。
- フューチャーでは、タスクの取り消し(cancelltion)を実装することもできる。取り消しは、非決定論性の分岐限定パターン(branch-and-bound pattem)や投機的選択(speculative selection) のような パターンの実装に使用できる。
3.6.3 投機的選択
投機的選択 (speculative selection)は、条件と両方の選択肢が並列に実行できるように選択を一般化する条件が満たされると、投機的選択の不要な分岐は取り消され(cancelled)ます。取り消しには、副作用の取り消しも含める必要がある。
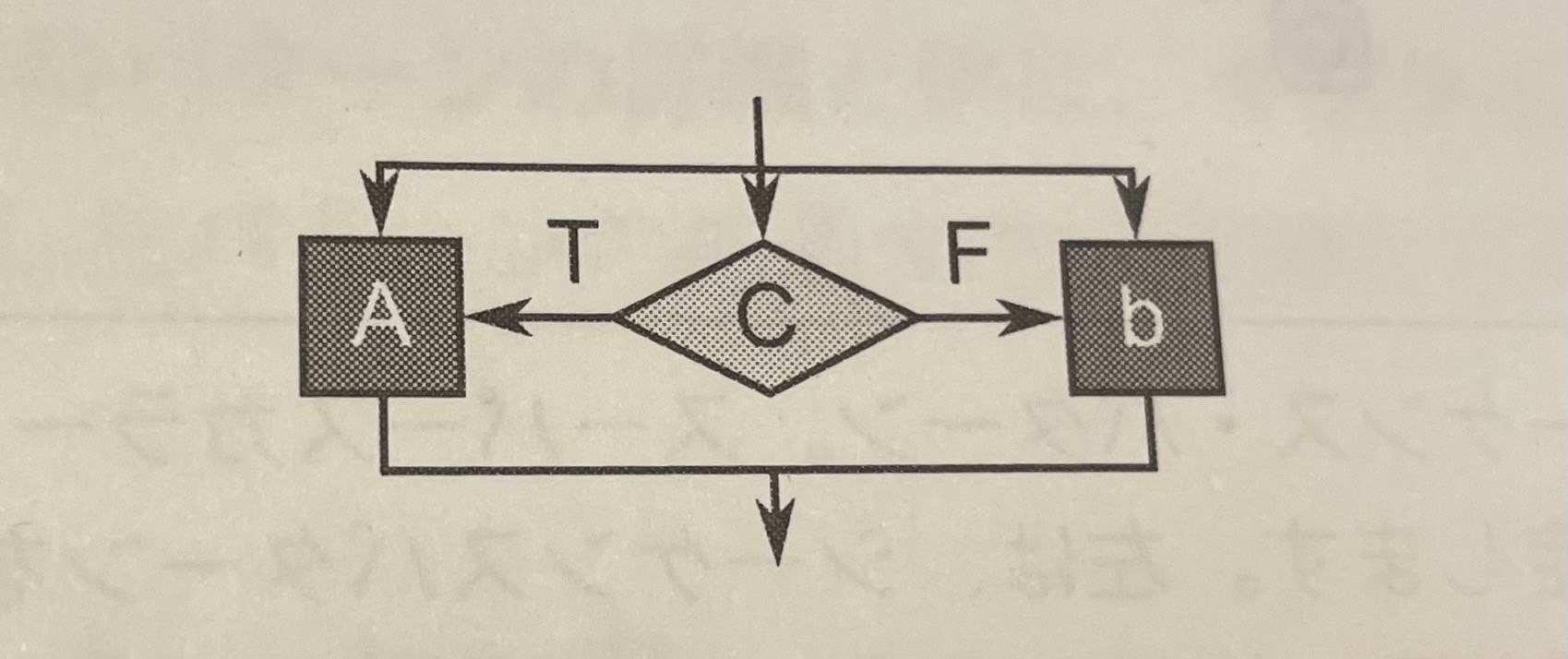
 図7
図7
- 取り消しの実装には、特にメモリーや副作用への変更を遅延する場合、コストがかかる。
- 投機的選択は、命令のレイテンシーを隠したり、SIMD マシンで複数のスレッドをシミュレーションするため、コンパイラーの非常に細かいスケールの並列処理によく使用される。
- このパターンは、一般にコンパイラーまたはハードウェアによって実装されるため、ほとんどの場合、細かいスケールでの使用に関して考慮する必要はない。実際、プロセッサーのアウトオブオーダー・ハードウェアはパフォーマンスが向上するため、消費電力と引き換えにこのパターンを頻繁に使用する。
- SIMTマシンモデルでは、制御フローの複数のスレッドは、マスクを使用してSIMDマシンでエミュレートされ、これは投機的選択に関連している。
- 同様のアプローチによりSIMDマシン上で反復をエミュレートできるが、反復の場合、ループの終了テストにはすべてtrueか、すべてfalseが使用される。どちらの場合も、大さなワークロードの小さなブロックにのみSIMDモデルを使用し、ブロックの管理にはスレッドモデルを使用すると良いだろう。
3.6.4 ワークパイル
ワークパイル・パターン(workpile pattern)は、要素関数の各インスタンスが複数のインスタンスを生成し、ワークの「パイル」に追加することができる、マップパターンの一般化のこと。このパターンは、例えば、ツリーの各ノードの子ごとにインスタンスを生成して処理する再帰ツリー検索に使用できる。 - ワークパイル・パターンはマップパターンよりもベクトル化が困難。
3.6.5. 検索
- 検索パターン (sanch pattern)は、コレクションから特定の条件に、一致するデータを見つける。結合配列のように特定のキーと完全に一致するような単純な条件や、論理的および算術的制約を満たすコレクション中の要素群のような複雑な条件を指定することができる。
- 多くの場合、検索はソートと関連付けられ、効率良く検索するには、データをソート順に維持することが望ましいためである。しかし、必ずしもこれが効率良い検察の実装に必須なわけではない。
3.6.6 セグメント化
- コレクションに対する操作は一般化して、セグメント化(segmentation)コレクションに利用できる。セグメント化コレクションとは、1次元配列をオーバーラップしない不均一なサイズのセグメントに分割したもの。スキャンとレデュースのような操作は、各セグメントに対する個別の操作として一般化できる。
- セグメントのサイズは均一ではないかもしれないが、セグメントのスキャンとリダクションは、セグメントのサイズに関係なく、規則的な方法で実装できる。
- セグメント化収集操作は、通常のリダクションとスキャンよりもコストがかかるが、ロードバランス(負荷均衡)とベクトル化を容易に行える。
3.6.7 展開
展開パターン(expand pattern) は、マップの各要素が選択的に要素を出力できるという点で、パックパターンとマップをマージしたものと考えることができる。しかし、展開パターンでは、マップの各要素はゼロ以上の任意の数の要素を出力することができる。要素は、マップの名選素によって生成された順に、それを生成したマップ要素の空間位置で並べられたセグメントで出力コレクションにパックされる。
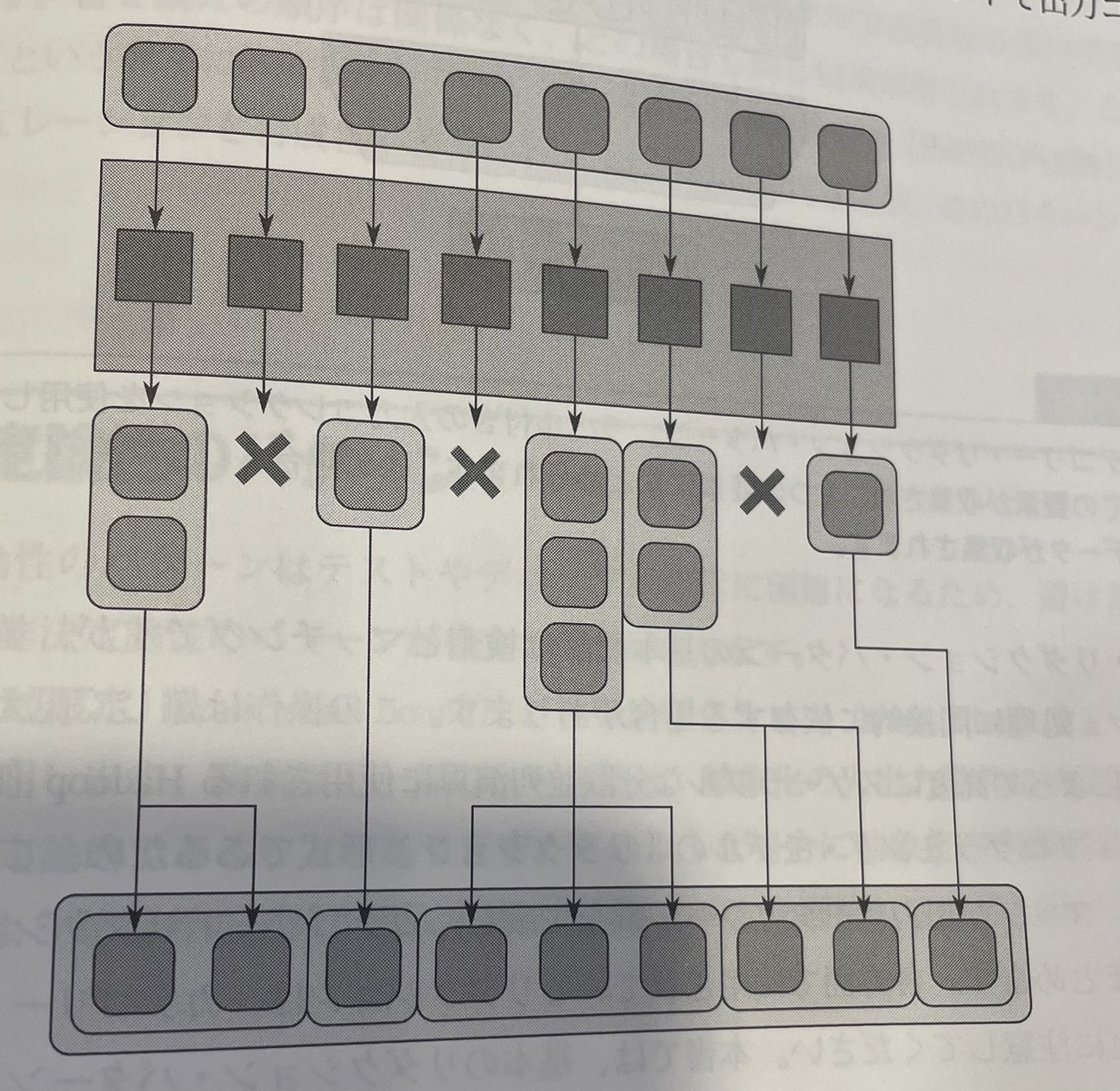
 図8
図8
3.6.8 カテゴリー・リダクション
カテゴリー・リダクション・パターン(category reduction pattern)は、要素ごとにラベルが付けられたデータ要素のコレクションを使用して、同じラベルのすべての要素を見つけ、結合演算子(可能な場合は可換でもある)を使ってそれらを1つの要素にまとめるというもの。
- 検索とセグメント化リダレクションの組み合わせとみなせる。
- 基本機能は検索とマッチングで、並列化がやや困難なソートやハッシュ処理に間接的に依存する可能性がある。
- カテゴリー・リダクションは、視覚分野におけるセグメント化領域の評価基準の計算、Web 分析の計算、マップ-レデュースを使用して実装されるその他多数のアプリケーションなどで使用される。
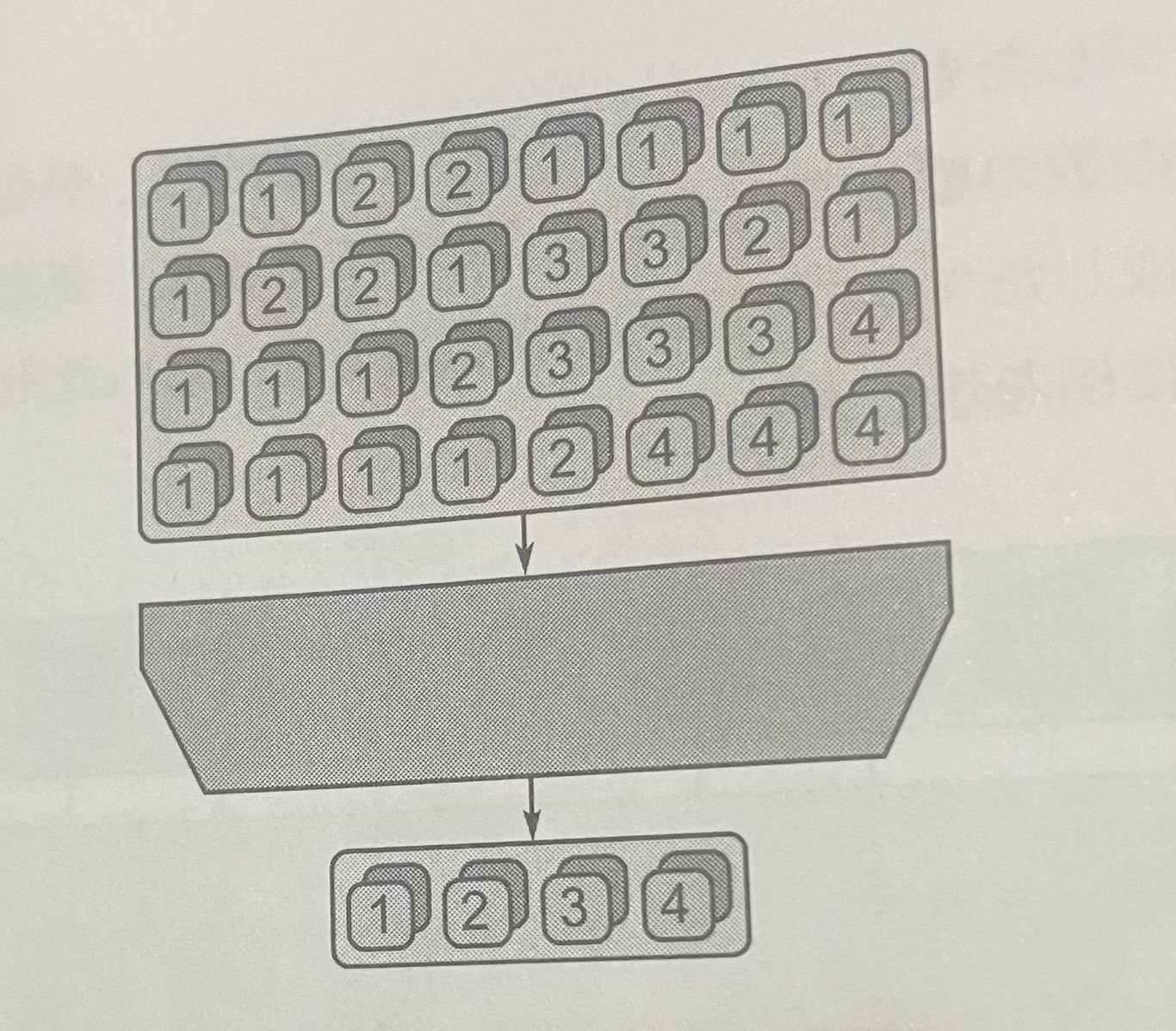
 図9
図9
3.6.9 項グラフ書き換え
項グラフ書き換えパターンは DAG (directed acyclic graph、有向非巡回グラフ)中のパターン、具体的には先頭ノードで指定される「項」と子のシーケンスを照合する。そして、これらの項を新しいサブグラフで置換する。
- グラフが最新状態になるまで置換する。
- 項グラフ書き換えは、関数型言語のセマンティクスの定義に使用されるラムダ演算式と同じ効果があるが、グラフ書き換えのほうが、グラフで直接表現されるため、データ共有の点では明験。
3.7 非決定論性のパターン
これらのパターンは通常デバッグやテストが大変なため避けるべき。しかし役立つ場面もある。
3.7.1 分岐限定
- 多くの場合非常に効果的な検索の実装に仕様される。
- ほかの多くの並列アルゴリズムと異なり、分岐限定戦路は実際に超線形スピードアップを実現できる。 これを実現できているのは、処理中のタスクを効率よく取り消す実装があるから。
具体的には...
定義城Yの最適値がyよりも劣っており、すでに見つかっている解xがyよりも優れていることを証明できれば、検索を取り消すことができる。この場合、Yのすべての検索を取り消せる。数学的に、区間解析[HW04]などの手法により増界を計算し、細分化限定アプローチを再帰的に適用できる。
3.7.2 トランザクション
- トランザクション (transaction)は、データの中央レポジトリーでいくつかの異なる更新が必要であり、レポジトリーが一貫した状態で維持される限り、任意の順序で更新を実行できる場合に使用される。
例として...
銀行口座取引のデータベースへの記録。ある口座のその日の最終残高が正しければ、入金と出金がどの順序で記録されるかはさほど重要ではない。 - トランザクションが有効な具体例として、ハッシュテーブルの利用が挙げられる。ハッシュテーブルを使用する操作には、要素の挿入や検索が含まれるため。 - 複数の並列タスクが同じバケットに要素を挿入する場合、リンクリストが一貫して更新されるように、トランザクション・パターンを使用することができる。
3.8 パターンのプログラミング・モデル・サポート
この章で説明したパターンの多くは、本書で取り上げるさまざまなプログラミング・モデルで直接サポートされている。直接サポートとは、パターンに対応する言語構造があることを意味する。その中でもCilk Plus、TBB、OpenMP、ArBB、OpenCLでサポートされるパターンを簡単に説明する。
シリアルパターンのサポートの概要を表3.1に、並列パターンのサポートの概要を表3.2と3.3に示す。これらの表で、「対応」はプログラミング・モデルにパターンをサポートする明確な機能が含まれている場合を、「実装可能」はプログラミング・モデルでパターンを実装可能な場合を、空白はプログラミング・モデルでパターンを実装する直接的な方法がない場合を示している。一部のパターンは、ほかのパターンを使用して実装することができ、そのような例を「間接」としている。表3.2には、パターンの使用例または実装例を紹介した節番号も記載。
表3.1
| シリアルパターン | TBB | Cilk Plus | OpenMP | ArBB | OpenCL |
|---|---|---|---|---|---|
| ネスト | 対応 | 対応 | 対応 | 対応 | 対応 |
| シーケンス | 対応 | 対応 | 対応 | 対応 | 対応 |
| 選択 | 対応 | 対応 | 対応 | 対応 | 対応 |
| 反復 | 対応 | 対応 | 対応 | 対応 | 対応 |
| 再帰 | 対応 | 対応 | 対応 | 不明 | |
| ランダムな読み込み | 対応 | 対応 | 対応 | 対応 | 対応 |
| ランダムな書き込み | 対応 | 対応 | 対応 | 対応 | |
| スタック割り当て | 対応 | 対応 | 対応 | 不明 | |
| ヒープ割り当て | 対応 | 対応 | 対応 | ||
| クロージャー | 対応 | 対応 | |||
| オブジェクト | 対応 | 対応 | 対応(C++) | 対応 |
表3.2
| 並列パターン | TBB | Cilk Plus | OpenMP | ArBB | OpenCL |
|---|---|---|---|---|---|
| 並列ネスト | 対応 | 対応 | |||
| マップ | 対応4.2.3; 4.3.3 11 | 対応4.2.4;4.2.5;4.3.4;4.3.5 11 | 対応4.2.6;4.3.6 | 対応4.2.7;4.2.8;4.3.7 | 対応4.2.9;4.3.8 |
| ステンシル | 実現可能 10 | 実現可能 10 | 実現可能 | 対応10 | 実現可能 |
| ワークパイル | 対応 | 実現可能 | |||
| リダクション | 対応5.3.4 11 | 対応5.3.5 11 | 対応5.3.6 | 対応5.3.7 | 実現可能 |
| スキャン | 対応5.6.5 14 | 実現可能5.6.3 間接8.11 14 | 実現可能5.6.4 間接5.4.4 | 対応5.6.6 | 実現可能 |
| フォーク・ジョイント | 対応 8.9.2 13 | 対応8.7;8.91 13 | 実現可能 | ||
| 繰り返し | 間接8.12 | ||||
| スーパースカラー・シーケンス | 対応 | ||||
| フューチャー | |||||
| 投機的選択 | |||||
| パック | 実現可能 14 | 実現可能 14 | 実現可能 | 対応 | 実現可能 |
| 展開 | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| パイプライン | 対応12 | 実現可能 12 | 実現可能 | ||
| 幾何学分解 | 実現可能 15 | 実現可能 15 | 実現可能 | 実現可能 | 実現可能 |
| 検索 | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| カテゴリー・リダクション | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| ギャザー | 実現可能 | 対応 | 実現可能 | 対応 | 実現可能 |
| アトミック・スキャッター | 対応 | 実現可能 | 実現可能 | ||
| 順列スキャッター | 対応 | 対応 | 対応 | 対応 | 対応 |
| マージ・スキャッター | 実現可能 | 実現可能 | 実現可能 | 対応 | 実現可能 |
| 優先スキャッター |
表3.3
| 並列パターン | TBB | Cilk Plus | OpenMP | ArBB | OpenCL |
|---|---|---|---|---|---|
| スーパースカラー・シーケンス | 実現可能 | 実現可能 | 実現可能 | 対応 | |
| フューチャー | 実現可能 | 実現可能 | 実現可能 | 実現可能 | |
| 投機的選択 | 実現可能 | ||||
| ワークパイル | 対応 | 実現可能 | 実現可能 | 実現可能 | |
| 展開 | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| 検索 | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| カテゴリー・リダクション | 実現可能 | 実現可能 | 実現可能 | 実現可能 | 実現可能 |
| アトミック・スキャッター | 対応 | 実現可能 | 実現可能 | 実現可能 | |
| 順列スキャッター | 対応 | 対応 | 対応 | 対応 | 対応 |
| マージ・スキャッター | 実現可能 | 実現可能 | 実現可能 | 対応 | 実現可能 |
| 優先スキャッター |
3.8.1 Cilk Plus
Cilk Plus の機能は、主にフォーク・ジョイン・パターンの効率良い実装に基づいた単純なものだが、一般的であるため、基本機能を用いてほかの多くのパターンを実装することができる。
特徴
- ビルトイン機能としてサポート。
- アトミック操作(atomic operation)やスケーラブルな並列動的メモリー割り当てが必要な場合、Cilk PlusとTBB のコンポーネントを組み合わせる必要がある。
- アトミック操作は情報工学 においていくつかの操作を組み合わもので、システムの他の部分から見てそれらがひとつの操作に見えるものをいう。
ネスト、再帰、フォーク・ジョイン
- 任意の深さのネストがcilk_spawnでサポートされている。特に、この構造は再帰を一般化するフォーク・ジョイン並列化をサポートする。
- Clik Plusのフォーク・ジョインは、大きな並列スラック(paralel slack、 全的な立列性の量)を簡単に表現し、限られたハードウェア・リソースに(ほとんどの場合は自動的に)効率良くマップするように実装される。
リダクション
- Clik Plusでは、ハイパーオプジェクト(hyperobjecr)により、一般的な方法でリダクション・パターンがサポートされる。ハイパーオブジェクトは、任意の結合操作および可換操作に基づいたりダクションをサポートする。
マップ、ワークパイル
- Cilk Plus では、cilk_forを使用してマップパターンを表現できる。ループ構文に適用されるが、cilk_forに変換することですべてのループを並列化できるわけではない。並列化するには、ループにループ伝搬依存があってはいけない。
- CilkPlus では、要素関数を使用してマップパターンを表現することもできる。
スキャッタ、ギャザー
CilK Plusの配列表記(アレイ・ノーテーション)は、スキャッター・パターンとギャザーパターンを直接サポートしている。
3.8.2 スレッディング・ビルディング・ブロック
スレッディング・ビルディング・ブロック(TBB) は、ワークステール負付バランサーを基本モデルとするフォーク・ジョインをサポートしている。
特徴
- Cilk Plusとは対照的に、TBBは可搬性があるISOに準拠したC++ライブラリーで、コンパイラー拡張ではない。TBBはコンパイラーと統合されないため、TBBのフォーク・ジョイン実装はCilk Plusほど効率的ではなく、またベクトル化を直接サポートできない。
- しかしTBBは、パイプラインのようにCilk Plusでは直接利用できない一部のパターンの実装を提供する。可搬性のあるライブラリーなので、現時点ではTBBのほうがCilk Plusよりも多くのプラットフォームで利用できる。
ネスト、再帰、フォーク・ジョイン
フォーク・ジョイン・モデルを介してタスクの任意の深さのネストをサポートする。Cilk Plusと同様に、スケーラブルで局所性を保持するワークスチール・ロードバランスを使用する。
マップ
Tparallel_for 関数と parallel_foreach 関数を使用してマップパターンを実装する。これらの関数の引数としてラムダ関数を使用できるため、必要な要素関数を個別に宣言する代わりに、呼び出しの一部として表現することができる。
ワークパイル
parallel_do構造を使用してワークパイル・パターンを利用できる。
リダクション
リダクション・パターンはparallel_reduce構造を介して利用できる。この構造では、任意の集約関数を指定できる。
スキャン
スキャンパターンはparallel_scan構造を介して利用できる。決定論性のある結果になるように、任意の後続関数を指定できる。リダクションと同様に、決定論性のあるスキャンにするには、後続関数は完全に結合則を満たし、かつ可換でなければいけない。
パイプライン
パイプライン・パターンは、parallel_pipeline構造を使用して直接指定できる。
投機的選択、分岐限定
タスクの取り消しをサポートしている。これは、分岐限定のような非決定論性パターンを含むほかの多くのパターンの実装で使用される。
3.8.3 OpenMP
OpenMPは、特定の構造(特にループ)が並列構造として再解釈されるように、シリアルコードをアノテーションするプログラミングの標準インターフェイスである。
特徴
- ベクトル化もサポートするデータ並列マップパターンに加えて、OpenMPの最新バージョンでは、より不規則なパターンを実装できる一般的なタスク構造もサポートしている。
- 特にOpenMPの実装はスレッドに直結しているため、様々な問題を引き起こす。特にOpenMPではネストパターンはサポートされていない。
- ワークユニットをスレッドに直接マップする OpenMPの機能により、タスクベースの自動負荷バランサーが使用できない。
- OpenMPが優れている点の1つは、Fortran、C,C++ で利用できること。
マップ、ワークパイル
for ループ(Fortran ではDOループ)に注釈を加え、コンパイラーに並列構造として解釈するように指示することでマップパターンをサポートしている。
リダクション
事前定義された結合演算子(または部分的に結合則を満たす浮動小数点演算子)を使用して、ループ本体の外側で宣言された変数をループ本体で更新する場合、その変数をリダクション変数として指示する。この場合、OpenMPは自動的に並列りダクションを行う。
フォーク・ジョイン
フォーク・ジョイン・パターンの実装に使用できる一般的なタスクモデルをサポートしている。タスクモデルは、ほかのさまざまなパターンの実装にも使用できる。
ステンシル、幾何学分解、ギャザー、スキャッター
OpenMPには、ステンシル、幾何学分解、ギャザー、スキャッターを直接表現できるビルトインサポートはないが、これらのパターンは、OpenMPで並列化される多くのアプリケーションで使用される。しかし、リダクション変数を除いて、OpenMPは一般にデータを管理しないため、データ・アクセス・パターンは、OpenMPではなく、言語の基本機能を使用して表現する。
3.8.4 アレイ・ビルディング・ブロック(ArBB)
ArBBの基本ビルディング・ブロックはこれまで説明してきた多くの基本パターンに基づいている。
特徴
- これらの基本ビルディング・ブロックの自動融合をサポートしており、ベクトル化されたコードと複数のコアで実行可能なコードを生成できる。
- ネストや再帰をサポートしていない。
マップ
マップパターンは、要素関数を使用してサポートされている。要素関数は個別に宣言し、コレクションまたはインデックス群のマップ操作で呼び出す必要がある。
リダクション、スキャン
リダクションは既知の演算子でのみサポートされる。スキャンパターンは、集合操作のscanとiscanを使用して、特定の演算子でサポートされる。現在の実装だと、集約が結合測を厳密に満たしてない場合、結果の決定論性は保証されない。
スキャッター、ギャザー
マップ内でスカラー読み込み/書き込みを使用するか、集合操作の gather と scatterを使用して、ランダムな読み込み/書き込みを実装できる。スキャッターの実装は、順列スキャッター・パターンのみサポートしている。可能な限り、スキャッターは避けるべき。
パック
集合操作のpackを使用して、バックパターンを直接サポートしている。パックの逆もunpack でサポートされている。packは安全で決定論性があり、多くの場合、スキャッターの代わりに使用できます。
3.8.5 OpenCL
OpenCLプログラミング・モデルは、個別のメモリーを持ち、GPUのようなタイルされたSIMDアーキテクチャーを採用する装着されたコプロセッサー(attached co-processor)を演算デバイスとして利用できるように設計されている。
特徴
- ネストを完全にサポートしていないが2つのレベルの並列性を提供する。
- デバイスの複数のコアにマップ。
- 各コアのSIMD レーンとハイパースレッド(hypertread)にマップ。
マップ
カーネル関数が、OpenCL で記述され、デバイス上で実行される場合、マップパターンを実装。これは、ArBBとCilk Plusの配列表記における要素関数に似ている。マップが実行されると、ワーク項目は、自動的にワークグループと呼ばれる並列ワークのセットにタイルされる。一般に、各ワークグループ内では、SIMD レーンのマスクを使用して、複数のワーク項目にわたる制御フローをエミュレートする。また、ワークグループ間ではできないが、ワークグループ内であれば共有メモリーを使用して通信すること可能。
ギャザー
- OpenCLカーネル内で、メモリーのランダムな読み込みを実行することができる。これは、オンチップのローカルメモリー(常に高速で、ワークグループ内で共有される)またはグローバルメモリーに対して行える。
- OpenCLを使用する目的は、レイテンシーを最小限にすることより、スループットを最大限にすること。ハイパースレッドとソフトウェア・パイプラインは、演算を追加してメモリー・アクセス。レイテンシーをオーバーラップさせるが、レイテンシーを排除するわけではない。実際、これらの手法を使用することで、全体のレイテンシーは増加する。
スキャッター
スキャッターはOpenCLでサポートされていますが、衝突(collision、同じアドレスへの並列書き込み)の扱いに注意する必要。OpenCLの最新バージョンではアトミック操作(atomicoperalion)が標準化されており、OpenCL 実装の対象プロセッサーの多くはハードウェアでこの機能をサポートしている。
リダクション、スキャン、パック、展開
- OpenCLは、リダクション・パターンを直接サポートしていないが、実装することは可能。
- スキャンもビルトイン機能はありませんが、効率良く実装する方法がいくつかある「Inco9a」。スキャンとギャザー/スキャッターが実装できるため、パックも実装することができる。
- 表3.2で「展開」は実装可能となっていたが、効率性のため、要素ごとの展開率を制限する必要がある。
ステンシル
ステンシルはOpenCLのビルトイン機能ではないが効率よく実装できる。キャッシュのないテバイス上でデータの再利用をサポートするには、明示的にローカルの共有メモリーを使用することが理想的
ワークパイル
ワークパイル・パターンは直接サポートしていないが、プログラミング・モデルが似ているCUDAのアトミックをしようしてワークキューを実装できる。
スーパースカラー・シーケンス
複数のカーネルをキューに追加し、OpenCLデバイスで非同期に実行することができる。カーネル間の依存性は、イベント形式で宣言できる。OpenCL自体はデータ依存を追跡しないが、データ依存に対応する適切なイベントが作成されれば、OpenCLはスーパースカラー・シーケンス・パターンを実装できる。
幾何学分解
OpenCLでは幾何学分解を実装できる。実際、パフォーマンス向上のため、幾何学分解が必要になるが、多くの場合、タイルをローカルの共有メモリーにマップするため、分解は1レベルに制限される。
クロージャー
OpenCLは動的コンパイルにより実装されるため、理論的にはランタイムに新しいカーネルを実装できます。しかし、この機能のインターフェイスは、カーネルの定義に文字列が使用されるため、ArBBのように使いやすくない。OpenCLはCに基づくため、オブジェクトはビルトイン機能ではない。また、OpenCLは一般にスタックも再帰もサポートしていない。
3.9 まとめ
パターンの概要を紹介し、並列プログラミングで役立つパターンを解説した。
- これらのパターンを構造化並列プログラミングで使用されるブロック制御フローのパターンに関連付けた。
- シリアルパターンではネストされた制御フロー構造を可能にし、並列プログラミングではネストされた並列性を実現する。
- プログラミング・モデルは、サポートする形態(ビルトイン機能による直接サポートか、ほかの機能を使用して簡単に効率良く実装できるか)によって分類できます。